§ 1.

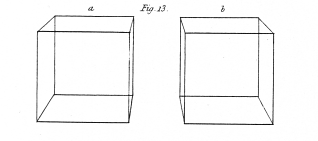
WHEN an object is viewed at so great a distance that the optic axes of both eyes are sensibly parallel when directed towards it, the perspective projections of it, seen by each eye separately, are similar, and the appearance to the two eyes is precisely the same as when the object is seen by one eye only. There is, in such case, no difference between the visual appearance of an object in relief and its perspective projection on a plane surface; and hence pictorial representations of distant objects, when those circumstances which would prevent or disturb the illusion are carefully excluded, may be rendered such perfect resemblances of the objects they are intended to represent as to be mistaken for them; the Diorama is an instance of this. But this similarity no longer exists when the object is placed so near the eyes that to view it the optic axes must converge; under these conditions a different perspective projection of it is seen by each eye, and these perspectives are more dissimilar as the convergence of the optic axes becomes greater. This fact may be easily verified by placing any figure of three dimensions, an outline cube for instance, at a moderate distance before the eyes, and while the head is kept perfectly steady, viewing it with each eye successively while the other is closed. Plate XI. fig. 13. represents the two perspective projections of a cube; b is that seen by the right eye, and a that presented to the left eye; the figure being supposed to be placed about seven inches immediately before the spectator.

The appearances, which are by this simple experiment rendered so obvious, may be easily inferred from the established laws of perspective; for the same object in relief is, when viewed by a different eye, seen from two points of sight at a distance from each other equal to the line joining the two eyes. Yet they seem to have escaped the attention of every philosopher and artist who has treated of the subjects of vision and perspective. I can ascribe this inattention to a phenomenon leading to the important and curious consequences, which will form the subject of the present communication, only to this circumstance; that the results being contrary to a principle which was very generally maintained by optical writers, viz. that objects can be seen single only when their images fall on corresponding points of the two retinæ, an hypothesis which will be hereafter discussed, if the consideration ever arose in their minds, it was hastily discarded under the conviction, that if the pictures presented to the two eyes are under certain circumstances dissimilar, their differences must be so small that they need not be taken into account.

It will now be obvious why it is impossible for the artist to give a faithful representation of any near solid object, that is, to produce a painting which shall not be distinguished in the mind from the object itself. When the painting and the object are seen with both eyes, in the case of the painting two similar pictures are projected on the retinæ, in the case of the solid object the pictures are dissimilar; there is therefore an essential difference between the impressions on the organs of sensation in the two cases, and consequently between the perceptions formed in the mind; the painting therefore cannot be confounded with the solid object.

After looking over the works of many authors who might be expected to have made some remarks relating to this subject, I have been able to find but one, which is in the Trattato della Pittura of LEONARDO DA VINCI * [* See also a Treatise of Painting, p. 178. London, 1721; and Dr. SMITH’S Complete System of Optics, vol. ii. r. 244, where the passage is quoted.]. This great artist and ingenious philosopher observes, “that a painting, though conducted with the greatest art and finished to the last perfection, both with regard to its contours, its lights, its shadows and its colours, can never show a relievo equal to that of the natural objects, unless these be viewed at a distance and with a single eye. For,” says he, “if an object C (Plate X. fig. 1.) be viewed by a single eye at A, all objects in the space behind it, included as it were in a shadow E C F cast by a candle at A, are invisible to the eye at A; but when the other eye at B is opened, part of these objects become visible to it; those only being hid from both eyes that are included, as it were, in the double shadow C D, cast by two lights at A and B, and terminated in D, the angular space E D G beyond D being always visible to both eyes. And the hidden space C D is so much the shorter, as the object C is smaller and nearer to the eyes. Thus the object C seen with both eyes becomes, as it were, transparent, according to the usual definition of a transparent thing; namely, that which hides nothing beyond it. But this cannot happen when an object, whose breadth is bigger than that of the pupil, is viewed by a single eye. The truth of this observation is therefore evident, because a painted figure intercepts all the space behind its apparent place, so as to preclude the eyes from the sight of every part of the imaginary ground behind it.”

Had LEONARDO DA VINCI taken, instead of a sphere, a less simple figure for the purpose of his illustration, a cube for instance, he would not only have observed that the object obscured from each eye a different part of the more distant field of view, but the fact would also perhaps have forced itself upon his attention, that the object itself presented a different appearance to each eye. He failed to do this, and no subsequent writer within my knowledge has supplied the omission; the projection of two obviously dissimilar pictures on the two retinæ when a single object is viewed, while the optic axes converge, must therefore be regarded as a new fact in the theory of vision.

§ 2.

It being thus established that the mind perceives an object of three dimensions by means of the two dissimilar pictures projected by it on the two retinæ, the following question occurs: What would be the visual effect of simultaneously presenting to each eye, instead of the object itself, its projection on a plane surface as it appears to that eye? To pursue this inquiry it is necessary that means should be contrived to make the two pictures, which must necessarily occupy different places, fall on similar parts of both retinæ. Under the ordinary circumstances of vision the object is seen at the concourse of the optic axes, and its images consequently are projected on similar parts of the two retinæ; but it is also evident that two exactly similar objects may be made to fall on similar parts of the two retinæ, if they are placed one in the direction of each optic axis, at equal distances before or beyond their intersection.

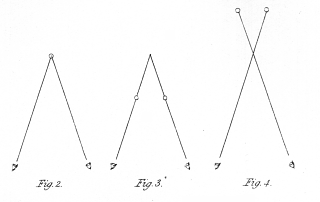
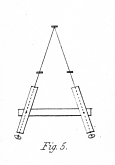
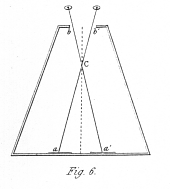
Fig. 2. represents the usual situation of an object at the intersection of the optic axes. In fig. 3. the similar objects are placed in the direction of the optic axes before their intersection, and in fig. 4. beyond it. In all these three cases the mind perceives but a single object, and refers it to the place where the optic axes meet. It will be observed, that when the eyes converge beyond the objects, as in fig. 3., the right hand object is seen by the right eye, and the left hand object by the left eye; while when the axes converge nearer than the Objects, the right hand object is seen by the left eye, and conversely. As both of these modes of vision are forced and unnatural, eyes unaccustomed to such experiments require some artificial assistance. If the eyes are to converge beyond the objects, this may be afforded by a pair of tubes (fig. 5.) capable of being inclined towards each other at various angles, so as to correspond with the different convergences of the optic axes. If the eyes are to converge at a nearer distance than that at which the objects are placed, a box (fig. 6.) may be conveniently employed; the objects a a' are placed distant from each other, on a stand capable of being moved nearer the eyes if required, and the optic axes being directed towards them will cross at c, the aperture b b' allowing the visual rays front the right hand object to reach the left eye, and those from the left hand object to fall on the right eye; the coincidence of the images may be facilitated by placing the point of a needle at the point of intersection of the optic axes c, and fixing the eyes upon it. In both these instruments (figs. 5. and 6.) the lateral images are hidden from view, and much less difficulty occurs in making the images unite than when the naked eyes are employed.

Now if, instead of placing two exactly similar objects to be viewed by the eyes in either of the modes above described, the two perspective projections of the same solid object be so disposed, the mind will still perceive the object to be single, but instead of a representation on a plane surface, as each drawing appears to be when separately viewed by that eye which is directed towards it, the observer will perceive a figure of three dimensions, the exact counterpart of the object from which the drawings were made. To make this matter clear I will mention one or two of the most simple cases.

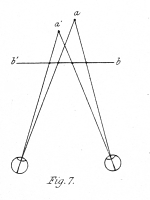
If two vertical lines near each other, but at different distances from the spectator, be regarded first with one eye and then with the other, the distance between them when referred to the same plane will appear different; if the left hand line be nearer to the eyes the distance as seen by the left eye will be less than the distance as seen by the right eye; fig. 7. will render this evident; a a' are vertical sections of the two original lines, and b b' the plane to which their projections are referred. Now if the two lines be drawn on two pieces of card, at the respective distances at which they appear to each eye, and these cards be afterwards viewed by either of the means above directed, the observer will no longer see two lines on a plane surface, as each card separately shows ; but two lines will appear, one nearer to him than the other, precisely as the original vertical lines themselves. Again, if a straight wire be held before the eyes in such a position that one of its ends shall be nearer to the observer than the other is, each eye separately referring it to a plane perpendicular to the common axis, will see a line differently inclined ; and then if lines having the same apparent inclinations be drawn on two pieces of card. and be presented to the eyes as before directed, the real position of the original line will be correctly perceived by the mind.

In the same manner the most complex figures of three dimensions may be accurately represented to the mind, by presenting their two perspective projections to the two retinæ. But I shall defer these more perfect experiments until I describe an instrument which will enable any person to observe all the phenomena in question with the greatest ease and certainty.

In the instruments above described the optic axes converge to some point in a plane before or beyond that in which the objects to be seen are situated. The adaptation of the eye, which enables us to see distinctly at different distances, and which habitually accompanies every different degree of convergence of the optic axes, does not immediately adjust itself to tIme new and unusual condition ; and to persons not accustomed to experiments of this kind, the pictures will either not readily unite, or will appear dim and confused. Besides this, no object can be viewed according to either mode when the drawings exceed in breadth the distance of the two points of the optic axes in which their centres are placed.

These inconveniences are removed by the instrument I am about to describe; the two pictures (or rather their reflected images) are placed in it at the true concourse of the optic axes, the focal adaptation of the eye preserves its usual adjustment, the appearance of lateral images is entirely avoided, and a large field of view for each eye is obtained. The frequent reference I shall have occasion to make to this instrument, will render it convenient to give it a specific name, I therefore propose that it be called a stereoscope, to indicate its property of representing solid figures.

§ 3.

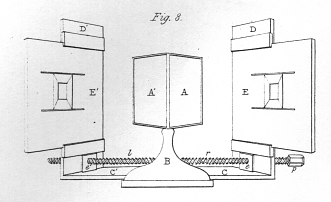
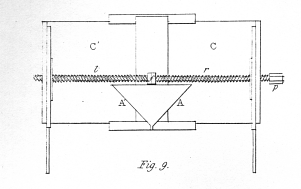
The stereoscope is represented by figs. 8. and 9; the former being a front view, and the latter a plan of the instrument. A A' are two plane mirrors, about four inches square, inserted in frames, and so adjusted that their backs form an angle of 90° with each other; these mirrors are fixed by their common edge against an upright B, or which was less easy to represent in the drawing, against the middle line of a vertical board, cut away in such manner as to allow the eyes to be placed before the two mirrors. C C' are two sliding boards, to which are attached the upright boards D D', which may thus be removed to different distances from the mirrors. In most of the experiments hereafter to be detailed, it is necessary that each upright board shall be at the same distance from the mirror which is opposite to it. To facilitate this double adjustment, I employ a right and a left-handed wooden screw, r l; the two ends of this compound screw pass through the nuts e e', which are fixed to the lower parts of the upright boards D D', so that by turning the screw pin p one way the two boards will approach, and by turning it the other they will recede from each other, one always preserving the same distance as the other from the middle line f. E E' are pannels, to which the pictures are fixed in such manner that their corresponding horizontal lines shall be on the same level: these pannels are capable of sliding backwards and forwards in grooves on the upright boards D D'. The apparatus having been described, it flow remains to explain the manner of using it. The observer must place his eyes as near as possible to the mirrors, the right eye before the right hand mirror, and the left eye before the left hand mirror, and he must move the sliding pannels E E' to or from him until the two reflected images coincide at the intersection of the optic axes, and form an image of the same apparent magnitude as each of the component pictures. The pictures will indeed coincide when the sliding pannels are in a variety of different positions, and consequently when viewed under different inclinations of the optic axes; but there is only one position in which the binocular image will be immediately seen single, of its proper magnitude, and without fatigue to the eyes, because in this position only the ordinary relations between the magnitude of the pictures on the retina, the inclination of the optic axes, and the adaptation of the eye to distinct vision at different distances are preserved. The alteration in the apparent magnitude of the binocular images, when these usual relations are disturbed, will be discussed in another paper of this series, with a variety of remarkable phenomena depending thereon. In all the experiments detailed in the present memoir I shall suppose these relations to remain undisturbed, and the optic axes to converge about six or eight inches before the eyes.

If the pictures are all drawn to be seen with the same inclination of the optic axes, the apparatus may be simplified by omitting the screw r 1 and fixing the upright boards D D' at the proper distances. The sliding pannels may also be dispensed with, and the drawings themselves be made to slide in the grooves.

§ 4.

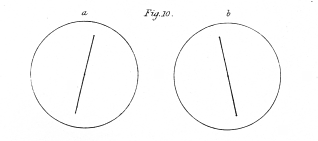
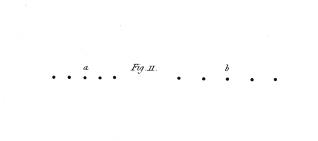
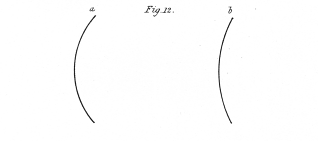
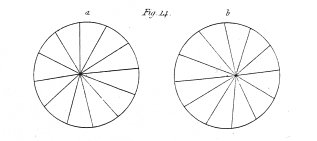
A few of outline figures, calculated to give rise to the perception of objects of three dimensions when placed in the stereoscope in the manner described, are represented from figs. 10. to 20. They are one half the linear size of the figures actually employed. As the drawings are reversed by reflection in the mirrors, I will suppose these figures to be the reflected images to which the eyes are directed in the apparatus; those marked b being seen by the right eye, and those marked a by the left eye. The drawings, it has been already explained, are two different projections of the same object seen from two points of sight, the distance between which is equal to the interval between the eyes of the observer; this interval is generally about 2½ inches.

a and b, fig. 10. will, when viewed in the stereoscope, present to the mind a line in the vertical plane, with its lower end inclined towards the observer. If the two component lines be caused to turn round their centres equally in opposite directions, the resultant line will, while it appears to assume every degree of inclination to the referent plane, still seem to remain in the same vertical plane.

Fig. 11. A series of points all in the same horizontal plane, but each towards the right hand successively nearer the observer.

Fig. 12. A curved line intersecting the referent plane, and having its convexity towards the observer.

Fig. 13. A cube.

Fig. 14. A cone, having its axis perpendicular to the referent plane, and its vertex towards the observer.

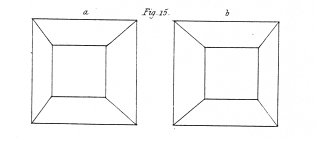
Fig. 15. The frustum of a square pyramid; its axis perpendicular to the referent plane, and its base furthest from the eye.

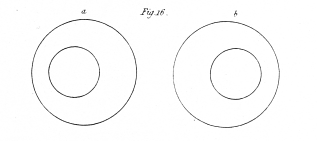
Fig. 16. Two circles at different distances from the eyes, their centres in the same perpendicular, forming the outline of the frustum of a cone.

The other figures require no observation.

For the purposes of illustration I have employed only outline figures, for had either shading or colouring been introduced it might be supposed that the effect was wholly or in part due to these circumstances, whereas by leaving them out of consideration no room is left to doubt that the entire effect of relief is owing to the simultaneous perception of the two monocular projections, one on each retina. But if it be required to obtain the most faithful resemblances of real objects, shadowing and colouring may properly be employed to heighten the effects. Careful attention would enable an artist to draw and paint the two component pictures, so as to present to the mind of the observer, in the resultant perception, perfect identity with the object represented. Flowers, crystals, busts, vases, instruments of various kinds, &c., might thus be represented so as not to be distinguished by sight from the real objects themselves.

It is worthy of remark, that the process by which we thus become acquainted with the real forms of solid objects, is precisely that which is employed in descriptive geometry, an important science we owe to the genius of MONGE, but which is little studied or known in this country. In this science, the position of a point, a right line or a curve, and consequently of any figure whatever, is completely determined by assigning its projections on two fixed planes, the situations of which are known, and which are not parallel to each other. In the problems of descriptive geometry the two referent planes are generally assumed to be at right angles to each other, but in binocular vision the inclination of these planes is less according as the angle made at the concourse of the optic axes is less ; thus the same solid object is represented to the mind by different pairs of monocular pictures, according as they are placed at a different distance before the eyes, and the perception of these differences (though we seem to be unconscious of them) may assist in suggesting to the mind the distance of the object. The more inclined to each other the referent planes are, with the greater accuracy are the various points of the projections referred to their proper places; and it appears to be a useful provision that the real forms of those objects which are nearest to us are thus more determinately apprehended than those which are more distant.

§ 5.

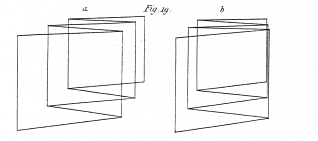
A very singular effect is produced when the drawing originally intended to be seen by the right eye is placed at the left hand sidle of the stereoscope, and that designed to be seen by the left eye is placed on its right hand side. A figure of three dimensions, as bold in relief as before, is perceived, but it has a different form from that which is seen when the drawings are in their proper places. There is a certain relation between the proper figure and this, which I shall call its converse figure. Those points which are nearest the observer in the proper figure are the most remote from him in the converse figure, and vice versâ, so that the figure is, as it were, inverted; but it is not an exact inversion, for the near parts of the converse figure appear smaller, and the remote parts larger than the same parts before the inversion. Hence the drawings which, properly placed, occasion a cube to be perceived, when changed in the manner described, represent the frustum of a square pyramid with its base remote from the eye: the cause of this is easy to understand.

This conversion of relief may be shown by all the pairs of drawings from fig. 10. to 19. In the case of simple figures like these the converse figure is as readily apprehended as the original one, because it is generally a figure of as frequent occurrence; hut in the vase of a more complicated figure, an architectural design, for instance, the mind, unaccustomed to perceive its converse, because it never occurs in nature, can find no meaning in it.

§ 6.

The same image is depicted on the retina by an object of three dimensions as by its projection on a plane surface, provided the point of sight remain in both cases the same. There should be, therefore, no difference in the binocular appearance of two drawings, one presented to each eye, and of two real objects so presented to the two eyes that their projections on the retina shall be the same as those arising from the drawings. The following experiments will prove the justness of this inference.

I procured several pairs of skeleton figures, i. e. outline figures of three dimensions, formed either of iron wire or of ebony beading about one tenth of an inch in thickness. The pair I most frequently employed consisted of two cubes, whose sides were three inches in length. When I placed these skeleton figures on stands before the two mirrors of the stereoscope, the following effects were produced, according as their relative positions were changed. 1st. When they were so placed that the pictures which their reflected images projected on the two retinæ were precisely the same as those which would have been projected by a cube placed at the concourse of the optic axes, a cube in relief appeared before the eyes. 2ndly. When they were so placed that their reflected images projected exactly similar pictures on the two retinæ, all effect of relief was destroyed, and the compound appearance was that of an outline representation on a plane surface. 3rdly. When the cubes were so placed that the reflected image of one projected on the left retina the same picture as in the first case was projected on the right retina, and conversely, the converse figure in relief appeared.

§7.

If a symmetrical object, that is one whose right and left sides are exactly similar to each other but inverted, be placed so that any point in the plane which divides it into these two halves is equally distant from the two eyes, its two monocular projections are, it is easy to see, inverted facsimiles of each other. Thus fig. 15, a and b are symmetrical monocular projections of the frustum of a four-sided pyramid, and figs. 13. 14. 16. are corresponding projections of other symmetrical objects. This being kept in view, I will describe an experiment which, had it been casually observed previous to the knowledge of the principles developed in this paper, would have appeared an inexplicable optical illusion.

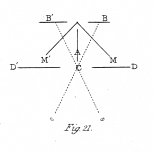
M and M' (fig. 21.) are two mirrors, inclined so that their faces form an angle of 90° with each other. Between them in the bisecting plane is placed a plane outline figure, such as fig. 15 a, made of card all parts but the lines being cut away, or of wire. A reflected image of this outline, placed at A, will appear behind each mirror at B and B', and one of these images will be the inversion of the other. If the eyes be made to converge at C, it is obvious that these two reflected images will fall on corresponding parts of the two retinæ, and a figure of three dimensions will be perceived; if the outline placed in the bisecting plane be reversed, the converse skeleton form will appear; in both these experiments we have the singular phenomenon of the conversion of a single plane outline into a figure of three dimensions. To render the binocular object more distinct, concave lenses may be applied to the eyes; and to prevent the two lateral images from being seen, screens may be placed at D and D'.

§ 8.

An effect of binocular perspective may be remarked in a plate of metal, the surface of which has been made smooth by turning it in a lathe. When a single candle is brought near such a plate, a line of light appears standing out from it, one half being above, and the other half below the surface; the position and inclination of this line chances with the situation of the light and of the observer, but it always passes through the centre of the plate. On closing the left eye the relief disappears, and the luminous line coincides with one of the diameters of the plate; on closing the right eye the line appears equally in the plane of the surface, but coincides with another diameter; on opening both eyes it instantly starts into relief * [* The luminous line seen by a single eye arises from the reflection of the light from each of the concentric circles produced in the operation of turning; when the plate is not large the arrangement of these successive reflections does not differ from a straight line.]. The case here is exactly analogous to the vision of two inclined lines (fig. 10.) when each is presented to a different eye in the stereoscope. It is curious, that an effect like this, which it must have been seen thousands of times, should never have attracted sufficient attention to have been made the subject of philosophic observation. It was one of the earliest facts which drew my attention to the subject I am now treating.

Dr. SMITH + [+ System of Optics, vol. ii. p. 388. and r. 526.] was very much puzzled by an effect of binocular perspective which he observed, but was unable to explain. He opened a pair of compasses, and while he held the joint in his hand, and the points outwards and equidistant from his eyes, and somewhat higher than the joint, he looked at a more distant point ; the compasses appeared double. He then compressed the legs until the two inner points coincided; having done this the two inner legs also entirely coincided, and bisected the angle formed by the outward ones, appearing longer and thicker than they did, and reaching from the hand to the remotest object in view. The explanation offered by Dr. SMITH accounts only for the coincidence of the points of the compasses, not for that of the entire leg. The effect in question is best seen by employing a pair of straight wires, about a foot in length. A similar observation, made with two flat rulers, and afterwards with silk threads, induced Dr. WELLS to propose a new theory of visible direction in order to explain it, so inexplicable did it seem to him by any of the received theories.

§ 9.

The preceding experiments render it evident that there is an essential difference in the appearance of objects when seen with two eyes, and when only one eye is employed, and that the most vivid belief of the solidity of an object of three dimensions arises from two different perspective projections of it being simultaneously presented to the mind. How happens it then, it may be asked, that persons who see with only one eye form correct notions of solid objects, and never mistake them for pictures? and how happens it also, that a person having the perfect use of both eyes, perceives no difference in objects around him when he shuts one of them? To explain these apparent difficulties, it must be kept in mind, that although the simultaneous vision of two dissimilar pictures suggests the relief of objects in the most vivid manner, yet there are other signs which suggest the same ideas to the mind, which, though more ambiguous than the former, become less liable to lead the judgment astray in proportion to the extent of our previous experience. The vividness of relief arising from the projection of two dissimilar pictures, one on each retina, becomes less and less as the object is seen at a greater distance before the eyes, and entirely ceases when it is so distant that the optic axes are parallel while regarding it. We see with both eyes all objects beyond this distance precisely as we see near objects with a single eye; for the pictures on the two retinæ are then exactly similar, and the mind appreciates no difference whether two identical pictures fall on corresponding parts of the two retinæ, or whether one eye is impressed with only one of these pictures. A person deprived of the sight of one eye sees therefore all external objects, near and remote, as a person with both eyes sees remote objects only, but that vivid effect arising from the binocular vision of near objects is not perceived by the former; to supply this deficiency he has recourse unconsciously to other means of acquiring more accurate information. The motion of the head is the principal means he employs. That the required knowledge may be thus obtained will be evident from the following considerations. The mind associates with the idea of a solid object every different projection of it which experience has hitherto afforded; a single projection may be ambiguous, from its being also one of the projections of a picture, or of a different solid object; but when different projections of the same object are successively presented, they cannot all belong to another object, and the form to which they belong is completely characterized. While the object remains fixed, at every movement of the head it is viewed from a different point of sight, and the picture on the retina consequently continually changes.

Every one must be aware how greatly the perspective effect of a picture is enhanced by looking at it with only one eye, especially when a tube is employed to exclude the vision of adjacent objects, whose presence might disturb the illusion. Seen under such circumstances from the proper point of sight, the picture projects the same lines, shades and colours on the retina, as the more distant scene which it represents would do were it substituted for it. The appearance which would make us certain that it is a picture is excluded from the sight, and the imagination has room to be active. Several of the older writers erroneously attributed this apparent superiority of monocular vision to the concentration of the visual power in a single eye * [* “We see more exquisitely with one eye shut than with both, because the vital spirits thus unite themselves the more, and become the stronger: for we may find by looking in a glass whilst we shut one eye, that the pupil of the other dilates.”—Lord BACON’S Works, Sylva Sylvarum, art. Vision.].

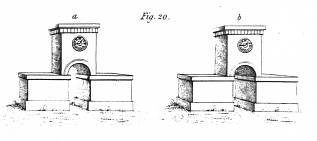
There is a well-known and very striking illusion of perspective which deserves a passing remark, because the reason of the effect does not appear to be generally understood. When a perspective of a building is projected on a horizontal plane, so that the point of sight is in a line greatly inclined towards the plane, the building appears to a single eye placed at the point of sight to be in bold relief, and the illusion is almost as perfect as in the binocular experiments described in §§ 2, 3, 4. This effect wholly arises from the unusual projection, which suggests to the mind more readily the object itself than the drawing of it; for we are accustomed to see real objects in almost every point of view, but perspective representations being generally made in a vertical plane with the point of sight in a line perpendicular to the plane of projection, we are less familiar with the appearance of other projections. Any other unusual projection will produce the same effect.

§ 10.

If we look with a single eye at the drawing of a solid geometrical figure, it may be imagined to be the representation of either of two dissimilar solid figures, the figure intended to be represented, or its converse figure (§ 5.). If the former is a very usual, and the latter a very unusual figure, the imagination will fix itself on the original without wandering to the converse figure; but if both are of ordinary occurrence, which is generally the case with regard to simple forms, a singular phenomenon takes place; it is perceived at one time distinctly as one of these figures, at another time as the other, and while one figure continues it is not in the power of the will to change it immediately.

The same phenomenon takes place, though less decidedly, when the drawing is seen with both eyes. Many of my readers will call to mind the puzzling effect of some of the diagrams annexed to the problems of the eleventh book of Euclid; which, when they were attentively looked at, changed in an arbitrary manner from one solid figure to another, and would obstinately continue to present the converse figures when the real figures alone were wanted. This perplexing illusion must be of coimmon occurrence, but I have only found one recorded observation relating to the subject. It is by Professor NECKER of Geneva, and I shall quote it in his own words from the Philosophical Magazine, Third Series, vol. i. p. 337.

“The object I have now to call your attention to is an observation which has often occurred to me while examining figures and engraved plates of crystalline forms; I mean a sudden and involuntary change in the apparent position of a crystal or solid represented in an engraved figure. What I mean will be more easily understood from the figure annexed (fig. 22.). The rhomboid A X is drawn so that the solid angle A should be seen the nearest to the spectator, and the solid angle X the farthest from him, and that the face A C D B should be the foremost, while the face X D C is behind. But in looking repeatedly at the same figure, you will perceive that at times the apparent position of the rhomboid is so changed that the solid angle X will appear the nearest, and the solid angle A the farthest; and that the face A C D B will recede behind the face X D C, which will come forward, which effect gives to the whole solid a quite contrary apparent inclination.”

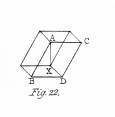
Professor NECKER attributes this alteration of appearance, not to a mental operation, but to an involuntary change in the adjustment of the eye for obtaining distinct vision. He supposed that whenever the point of distinct vision on the retina is directed on the angle A, for instance, this angle seen more distinctly than the others is naturally supposed to be nearer and foremost, while the other angles seen indistinctly are supposed to be farther and behind, and that the reverse takes place when the point of distinct vision is brought to bear on the angle X.

That this is not the true explanation, is evident from three circumstances: in the first place, the two points A and X being both at the same distance from the eyes, the same alteration of adjustment which would make one of them indistinct would make the other so ; secondly, the figure will undergo the same changes whether the focal distance of the eye be adjusted to a point before or beyond the plane in which the figure is drawn; and thirdly, the change of figure frequently occurs while the eye continues to look at the same angle. The effect seems entirely to depend on our mental contemplation of the figure intended to be represented, or of its converse. By following the lines with the eye with a clear idea of the solid figure we are describing, it may be fixed for any length of time; but it requires practice to do this or to change the figure at will. As I have before observed, these effects are far more obvious when the figures are regarded with one eye only.

No illusion of this kind can take place when an object of three dimensions is seen with both eyes while the optic axes make a sensible angle with each other, because the appearance of the two dissimilar images, one to each eye, prevents the possibility of mistake. But if we regard an object at such a distance that its two projections are sensibly identical, and if this projection be capable of a double interpretation, the illusion may occur. Thus a placard on a pole carried in the streets, with one of its sides inclined towards the observer, will, when he is distant from it, frequently appear inclined in a contrary direction. Many analogous instances might be adduced, but this will suffice to call others to mind ; it must however be observed, that when shadows, or other means capable of determining the judgement are present, these fallacies do not arise.

§ 11.

The same indetermination of judgement which causes a drawing to be perceived by the mind at different times as two different figures, frequently gives rise to a false perception when objects in relief are regarded with a single eye. The apparent conversion of a cameo into an intaglio, and of an intaglio into a cameo, is a well-known instance of this fallacy in vision; but the fact does not appear to me to have been correctly explained, nor the conditions under which it occurs to have been properly stated.

This curious illusion, which has been the subject of much attention, was first observed at one of the early meetings of the Royal Society * [* BIRCH’S History, vol. ii. p. 348.]. Several of the members looking through a compound microscope of a new construction at a guinea, some of them imagined the image to be depressed, while others thought it to be embossed, as it really was. Professor GMELIN, of Wurtemburg, published a paper on the same subject in the Philosophical Transactions for 1745 ; his experiments were made with telescopes and compound microscopes which inverted the images; and he observed that the conversion of relief appeared in some cases and not in others, at some times and not at others, and to some eyes also and not to others. He endeavoured to ascertain some of the conditions of the two appearances; “but why these things should so happen,” says he, “I do not pretend to determine.”

Sir DAVID BREWSTER accounts for the fallacy in the following manner + [+ Natural Magic, p. 100.] :— “A hollow seal being illuminated by a window or a candle, its shaded side is of course on the same side with the light. If we now invert the seal with one or more lenses, so that it may look in the opposite direction, it will appear to the eye with the shaded side furthest from the window. But as we know that the window is still on our left hand, and as every body with its shaded side furthest from the light must necessarily be convex or protuberant, we immediately believe that the hollow seal is now a cameo or bas-relief. The proof which the eye thus receives of the seal being raised, overcomes the evidence of its being hollow, derived from our actual knowledge and from the sense of touch. In this experiment the deception takes place from our knowing the real direction of the light which falls on the seal ; for if the place of the window, with respect to the seal, had been inverted as well as the seal itself, the illusion could not have taken place. The illusion, therefore, under our consideration is the result of an operation of our own minds, whereby we judge of the forms of bodies by the knowledge we have acquired of light and shadow. Hence the illusion depends on the accuracy and extent of our knowledge on this subject; and while some persons are under its influence, others are entirely insensible to it.”

These considerations do not fully explain the phenomenon, for they suppose that the image must be inverted, and that the light must fall in a particular direction but the conversion of relief will still take place when the object is viewed through an open tube without any lenses to invert it, and also when it is equally illuminated in all parts. The true explanation I believe to be the following. If we suppose a cameo and an intaglio of the same object, the elevations of the one corresponding exactly to the depressions of the other; it is easy to show that the projection of either on the retina is sensibly the same. When the cameo or the intaglio is seen with both eyes, it is impossible to mistake an elevation for a depression, for reasons which have been already amply explained; but when either is seen with one eye only, the most certain guide of our judgement, viz. the presentation of a different picture to each eye, is wanting; the imagination therefore supplies the deficiency, and we conceive the object to be raised or depressed according to the dictates of this faculty. No doubt in such cases our judgement is in a great degree influenced by accessory circumstances, and the intaglio or the relief may sometimes present itself according to our previous knowledge of the direction in which the shadows ought to appear; but the real cause of the phenomenon is to be found in the indetermination of the judgement arising from our more perfect means of judging being absent.

Observers with the microscope must be particularly on their guard against illusions of this kind. RASPAIL observes * [* Nouveau Système de Chimie Organique, 2me edit. t. 1. p. 333.] that the hollow pyramidal arrangement of the crystals of muriate of soda appears, when seen through a microscope, like a striated pyramid in relief. He recommends two modes of correcting the illusion. The first is to bring successively to the focus of the instrument the different parts of the crystal; if the pyramid be in relief, the point will arrive at the focus sooner than the base will; if the pyramid be hollow, the contrary will take place. The second mode is to project a strong light on the pyramid in the field of view of the microscope, and to observe which sides of the crystal are illuminated, taking however the inversion of the image into consideration if a compound microscope be employed.

The inversion of relief is very striking when a skeleton cube is looked at with one eye, and the following singular results may in this case be observed. So long as the mind perceives the cube, however the figure be turned about, its various appearances will be but different representations of the same object, and the same primitive form will be suggested to the mind by all of them: but it is not so if the converse figure fixes the attention; the series of successive projections cannot then be referred to any figure to which they are all common, and the skeleton figure will appear to be continually undergoing a change of shape.

§ 12.

I have given ample proof that objects whose pictures do not fall on corresponding points of the two retinæ may still appear single. I will now adduce an experiment which proves that similar pictures falling on corresponding points of the two retinæ may appear double and in different places.

Present, in the stereoscope, to the right eye a vertical line, and to the left eye a line inclined some degrees from the perpendicular (fig. 23.); the observer will then perceive, as formerly explained, a line, the extremities of which appear at different distances before the eyes. Draw on the left hand figure a faint vertical line exactly corresponding in position and length to that presented to the right eye; and let the two lines of this left hand figure intersect each other at their centres. Looking now at these two drawings in the stereoscope, the two strong lines, each seen by a different eye, will coincide, and the resultant perspective line will appear to occupy the same place as before; but the faint line which now falls on a line of the left retina, which corresponds with the line of the might retina on which one of the coinciding strong lines, viz. the vertical one, falls, appears in a different place. The place this faint line apparently occupies is the intersection of that plane of visual direction of the left eye in which it is situated, with the plane of visual direction of the right eye, which contains the strong vertical line.

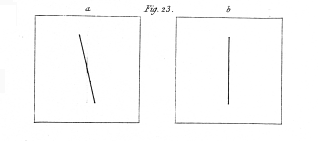
This experiment affords another proof that there is no necessary physiological connection between the corresponding points of the two retinæ,—a doctrine which has been maintained by so many authors.

§ 13. Binocular Vision of Images of different Magnitudes.

We will now inquire what effect results from presenting similar images, differing only in magnitude, to analogous parts of the two retinæ. For this purpose two squares or circles, differing obviously but not extravagantly in size, may be drawn on two separate pieces of paper, and placed in the stereoscope so that the reflected image of each shall he equally distant from the eye by which it is regarded. It will then be seen that, notwithstanding this difference, they coalesce and occasion a single resultant perception. The limit of the difference of size within which the single appearance subsists may be ascertained by employing two images of equal magnitude, and causing one of them to recede from the eye while the other remains at a constant distance ; this is effected merely by pulling out the sliding board C (fig. 8.) while the other C' remains fixed, the screw having previously been removed.

Though the single appearance of two images of different size is by this experiment demonstrated, the observer is unable to perceive what difference exists between the apparent magnitude of the binocular image and that of the two monocular images to determine this point the stereoscope must be dispensed with, and the experiment so arranged that all three shall be simultaneously seen ; which may be done in the following manner:—The two drawings being placed side by side on a plane before the eyes, the optic axes must be made to converge to a nearer point as at fig. 4., or to a more distant one as at fig. 3., until the three images are seen at the same time, the binocular image in the middle, and the monocular images at each side. It will thus be seen that the binocular image is apparently intermediate in size between the two monocular ones.

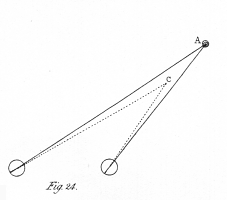
If the pictures be too unequal in magnitude, the binocular coincidence does not take place. It appears that if the inequality of the pictures be greater than the difference which exists between the two projections of the same object when seen in the most oblique position of the eyes (i. e. both turned to the extreme right or to the extreme left), ordinarily employed, they do not coalesce. Were it not for the binocular coincidence of two images of different magnitude, objects would appear single only when the optic axes converge immediately forwards; for it is only when the converging visual lines form equal angles with the visual base (the line joining the centres of the two eyes) as at fig. 2., that the two pictures can be of equal magnitude; but when they form different angles with it, as at fig. 24., the distance from the object to each eye is different, and consequently the picture projected on each retina has a different magnitude. If a piece of money be held in the position a, (fig. 24.) while the optic axes converge to a nearer point c, it will appear double, and that seen by the left eye will be evidently smaller than the other.

§ 14. Phenomena which are observed when objects of different forms are simultaneously presented to corresponding parts of the two retinæ.

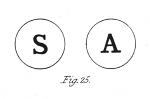
If we regard a picture with the right eye alone for a considerable length of time it will be constantly perceived; if we look at another and dissimilar picture with the left eye alone its effect will be equally permanent; it might therefore be expected, that if each of these pictures were presented to its corresponding eye at the same time the two would appear permanently superposed on each other. This, however, contrary to expectation, is not the case.

If a and b (fig. 25.) are each presented at the same time to a different eye, the common border will remain constant, while the letter within it will change alternately from that which would be perceived by the right eye alone to that which would be perceived by the left eye alone. At the moment of change the letter which has just been seen breaks into fragments, while fragments of the letter which is about to appear mingle with them, and are immediately after replaced by the entire letter. It does not appear to be in the power of the will to determine the appearance of either of the letters, but the duration of the appearance seems to depend on causes which are under our control: thus if the two pictures be equally illuminated, the alternations appear in general of equal duration; but if one picture be in ore illuminated than the other, that which is less so will be perceived during a shorter time. I have generally made this experiment with the apparatus, fig. 6. When complex pictures are employed in the stereoscope, various parts of them alternate differently.

There are some facts intimately connected with the subject of the present article which have already been frequently observed. I allude to the experiments, first made by DU TOUR, in which two different colours are presented to corresponding parts of the two retinæ. If a blue disc be presented to the right eye and a yellow disc to the corresponding part of the left eye, instead of a green disc which would appear if these two colours had mingled before their arrival at a single eye, the mind will perceive the two colours distinctly one or the other alternately predominating either partially or wholly over the disc. In the same manner the mind perceives no trace of violet when red is presented to one eye and blue to the other, nor any vestige of orange when red and yellow are separately presented in a similar manner. These experiments may be conveniently repeated by placing the coloured discs in the stereoscope, but they have been most usually made by looking at a white object through differently coloured glasses, one applied to each eye.

In some authors we find it stated, contrary to fact, that if similar objects of different colour be presented one to each eye, the appearance will be that compounded of the two colours. Dr. REID * [* Enquiry, Sect. xiii.] and JANIN are among the writers who have fallen into this inconsiderate error, which arose no doubt from their deciding according to previous notions, instead of ascertaining by experiment what actually does happen.

§ 15.

No question relating to vision has been so much debated as the cause of the single appearance of objects seen by both eyes. I shall in the present section give a slight review of the various theories which have been advanced by philosophers to account for this phenomenon, in order that the remarks I have to make in the succeeding section may be properly understood.

The law of visible direction for monocular vision has been variously stated by different optical writers. Some have maintained with Dr’s. REID and PORTERFIELD, that every external point is seen in the direction of a line passing from its picture on the retina through the centre of the eye; while others have supposed with Dr. SMITH that the visible direction of an object coincides with the visual ray, or the principal ray of the pencil which flows from it to the eye. D’ALEMBERT, furnished with imperfect data respecting the refractive densities of the humours of the eye, calculated that the apparent magnitudes of objects would differ widely on the two suppositions, and concluded that the visible point of an object was not seen in either of these directions, but sensibly in the direction of a line joining the point itself and its image on the retina; but he acknowledged that he could assign no reason for this law. Sir DAVID BREWSTER, provided with more accurate data, has shown that these three lines so nearly coincide with each other, that “at an inclination of 30°, a line perpendicular to the point of impression on the retina passes through the common centre, and does not deviate from the real line of visible direction more than half a degree, a quantity too small to interfere with the purposes of vision.” We may, therefore, assume in all our future reasonings the truth of the following definition given by this eminent philosopher :—“ As the interior eye-ball is as nearly as possible a perfect sphere, lines perpendicular to the surface of the retina must all pass through one single point, namely the centre of its spherical surface. This one point may be called the centre of visible direction, because every point of a visible object will be seen in the direction of a line drawn from this centre to the visible point.”

It is obvious, that the result of any attempt to explain the single appearance of objects to both eyes, or, in other words, the law of visible direction for binocular vision, ought to contain nothing inconsistent with the law of visible direction for monocular vision.

It was the opinion of AGUILONIUS, that all objects seen at the same glance with both eyes appear to be in the plane of the horopter. The horopter he defines to be a line drawn through the point of intersection of the optic axes, and parallel to the line joining the centres of the two eyes; the plane of the horopter to be a plane passing through this line at right angles to that of the optic axes. All objects which are in this plane, must, according to him, appear single because the lines of direction in which any point of an object is seen coincide only in this plane and nowhere else; and as these lines can meet each other only in one point, it follows from the hypothesis, that all objects not in the plane of the horopter must appear double, because their lines of direction intersect each other, either before or after they pass through it. This opinion was also maintained by DECHALES and PORTERFIELD. That it is erroneous, I have given, I think, sufficient proof, in showing that, when the optic axes converge to any point, objects before or beyond the plane of the horopter are under certain circumstances equally seen single as those in that plane.

Dr. WELLS’S “new theory of visible direction” was a modification of the preceding hypothesis. This acute writer held with AGUILONIUS, that objects are seen single only when they are in the plane of the horopter, and consequently that they appear double when they are either before or beyond it; but he attempted to make this single appearance of objects only in the plane of the horopter to depend on other principles, from which he deduced, contrary to AGUILONIUS, that the objects which are doubled do not appear in the plane of the horopter, but in other places which are determined by these principles. Dr. WELLS was led to his new theory by a fact which he accidentally observed, and which he could not reconcile with any existing theory of visible direction ; this fact had, though he was unaware of it, been previously noticed by Dr. SMITH; it is already mentioned in § 8., and is the only instance of binocular vision of relief which I have found recorded previous to my own investigations. So little does Dr. WELLS’S theory appear to have been understood, that no subsequent writer has attempted either to confirm or disprove his opinions. It would be useless here to discuss the principles of this theory, which was framed to account for an anomalous individual fact, since it is inconsistent with the general rules on which that fact has been now shown to depend. Notwithstanding these erroneous views, the “essay upon single vision with two eyes” contains many valuable experiments and remarks, the truth of which are independent of the theory they were intended to illustrate.

The theory which has obtained greatest currency is that which assumes that an object is seen single because its pictures fall on corresponding points of the two retinæ, that is on points which are similarly situated with respect to the two centres both in distance and position. This theory supposes that the pictures projected on the retinæ are exactly similar to each other, corresponding points of the two pictures falling on corresponding points of the two retinæ. Authors who agree with regard to this property, differ widely in explaining why objects are seen in the same place, or single, according to this law. Dr. SMITH makes it to depend entirely on custom, and explains why the eyes are habitually directed towards an object so that its pictures fall on corresponding parts in the following manner:—“ When we view an object steadily, we have acquired a habit of directing the optic axes to the point in view; because its pictures falling upon the middle points of the retinas, are then distincter than if they fell upon any other places; and since the pictures of the whole object are equal to one another, and are both inverted with respect to the optic axes, it follows that the pictures of any collateral point are painted upon corresponding points of the retinas.”

Dr. REID, after a long dissertation on the subject, concludes, “that by an original property of human eyes, objects painted upon the centres of the two retinæ, or upon points similarly situated with regard to the centres, appear in the same visible place; that the most plausible attempts to account for this property of the eyes have been unsuccessful ; and therefore, that it must be either a primary law of our constitution, or the consequence of some more general law which is not yet discovered.”

Other writers who have admitted this principle have regarded it as arising from anatomical structure and dependent on connexion of nervous fibres; among these stand the names of GALEN, Dr. BRIGGS, Sir ISAAC NEWTON, ROHAULT, Dr. HARTLEY, Dr. WOLLASTON and Professor MÜLLER.

Many of the supporters of the theory of corresponding points have thought, or rather have admitted, without thinking, that it was not inconsistent with the law of AGUILONIUS; but very little reflection will show that both cannot be maintained together; for corresponding lines of visible direction, that is, lines terminating in corresponding points of the two retinæ, cannot meet in the plane of the horopter unless the optic axes be parallel, and the plane be at an infinite distance before the eyes. Some of the modern German writers * [* Tortual, die Sinne des Menschen. Münster, 1827. Bartels, Beitrage zur Physiologie der Gesichtssinnes. Berlin, 1834.] have inquired what is the curve in which objects appear single while the optic axes are directed to a given point, on the hypothesis that objects are seen single only when they fall on corresponding points of the two retinæ. An elegant proposition has resulted from their investigations, which I shall need no apology for introducing in this place, since it has not yet been mentioned in any English work.

R and L (fig. 26.) are the two eyes; C A, C' A the optic axes converging to the point A; and C A B C' is a circle drawn through the point of convergence A and the centres of visible direction C C'. If any point be taken in the circumference of this circle, and lines be drawn from it through the centres of the two eyes C C', these lines will fall on corresponding points of the two retinæ D D'; for the angles A C B, A C' B being equal, the angles D C E, D C' E are also equal; therefore any point placed in the circumference of the circle C A B C' will, according to the hypothesis, appear single while the optic axes are directed to A, or any other part in it.

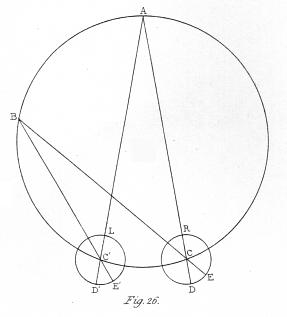
I will mention two other properties of this binocular circle: 1st. The arc subtended by two points on its circumference contains double the number of degrees of the arc subtended by the pictures of these points on either retina, so that objects which occupy 180° of the supposed circle of single vision are painted on a portion of the retina extended over 90° only; for the angle D C E or D C' E being at the centre, and the angle B C A or B C' A at the circumference of a circle, this consequence follows. 2ndly. To whatever point of the circumference of the circle the optic axes be made to converge, they will form the same angle with each other; for the angles C A C', C B C are equal.

In the eye itself, the centre of visible direction, or the point at which the principal rays cross each other, is, according to Dr. YOUNG and other eminent optical writers, at the same time the centre of the spherical surface of the retina, and that of the lesser spherical surface of the cornea; in the diagram (fig. 26.), to simplify the consideration of the problem, R and L represent only the circle of curvature of the bottom of the retina, but the reasoning is equally true in both cases.

The same reasons, founded on the experiments in this memoir, which disprove the theory of AGUILONIUS, induce me to reject the law of corresponding points as an accurate expression of the phenomena of single vision. According to the former, objects can appear single only in the plane of the horopter; according to the latter, only when they are in the circle of single vision; both positions are inconsistent with the binocular vision of objects in relief, the points of which they consist appearing single though they are at different distances before the eyes. I have already proved that the assumption made by all the maintainers of the theory of corresponding points, namely that the two pictures projected by any object in the retinæ are exactly similar, is quite contrary to fact in every case except that in which the optic axes are parallel.

GASSENDUS, PORTA, TACQUET and GALL maintained, that we see with only one eye at a time though both remain open, one according to them being relaxed and inattentive to objects while the other is upon the stretch. It is a sufficient refutation of this hypothesis, that we see an object double when one of the optic axes is displaced either by squinting or by pressure on the eye-ball with the finger; if we saw with only one eye, one object only should under such circumstances be seen. Again, in many cases which I have already explained, the simultaneous affection of the two retinæ excites a different idea in the mind to that consequent on either of the single impressions, the latter giving rise to the idea of a representation on a plane surface, the former to that of an object in relief; these things could not occur did we see with only one eye at a time.

Du TOUR * [* Act. Par. 1743. M. p. 334.] held that though we might occasionally see at the same time with both eyes, yet the mind cannot be affected simultaneously by two corresponding points of the two images. He was led to this opinion by the curious facts alluded to in § 14. It would be difficult to disprove this conjecture by experiment; but all that the experiments adduced in its favour, and others relating to the disappearance of objects to one eye really proves, is, that the mind is inattentive to impressions made on one retina when it cannot combine the impressions on the two retinæ together so as to resemble the perception of some external objects; but they afford no ground whatever for supposing that the mind cannot under any circumstances attend to impressions made simultaneously on points of the two retinæ, when they harmonize with each other in suggesting to the mind the same idea.

A perfectly original theory has been recently advanced by M. LEHOT + [+ Nouvelle Théorie de la Vision, Par. 1823.], who has endeavoured to prove, that instead of pictures on the retinæ, images of three dimensions are formed in the vitreous humour which we perceive by means of nervous filaments extended thence from the retina. This theory would account for the single appearance to both eyes of objects in relief, but it would be quite insufficient to explain why we perceive an object of three dimensions when two pictures of it are presented to the eyes; according to it, also, no difference should be perceived in the relief of objects when seen by one or both eyes, which is contrary to what really happens. The proofs, besides, that we perceive external objects by means of pictures on the retinæ are so numerous and convincing, that a contrary conjecture cannot be entertained for a moment. On this account it will suffice merely to mention two other theories which place the seat of vision in the vitreous humour. VALLEE ++ [++ Traité de la Science du Dessein, Par. 1821, p. 270.], without denying the existence of pictures on the retina, has advocated that we see the relief of objects by means of anterior foci on the hyaloid membrane; and RASPAIL § [§ Nouveau Système de Chimie Organique, t. 2. p. 329.] has developed at considerable length the strange hypothesis, that images are neither formed in the vitreous humour nor painted on the retina, but are immediately perceived at the focus of the lenticular system of which the eye is formed.

§ 16.

It now remains to examine why two dissimilar pictures projected on the two retinaæ give rise to the perception of an object in relief. I will not attempt at present to give the complete solution of this question, which is far from being so easy as at a first glance it may appear to be, and is indeed one of great complexity. I shall in this place merely consider the most obvious explanations which might be offered, and show their insufficiency to explain the whole of the phenomena.

It may be supposed that we see but one point of an object distinctly at the same instant, the one namely to which the optic axes are directed, while all other points are seen so indistinctly, that the mind does not recognize them to be either single or double, and that the figure is appreciated by successively directing the point of convergence of the optic axes successively to a sufficient number of its points to enable us to judge accurately of its form.

That there is a degree of indistinctness in those parts of the field of view to which the eyes are not immediately directed, and which increases with the distance from that point, cannot be doubted, and it is also true that the objects thus obscurely seen are frequently doubled. It may be said, this indistinctness and duplicity is not attended to, because the eyes shifting continually from point to point, every part of the object is successively rendered distinct; and the perception of the object is not the consequence of a single glance, during which only a small part of it is seen distinctly, but is formed from a comparison of all the pictures successively seen while the eyes are changing from one point of the object to another.

All this is in some degree true; but were it entirely so, no appearance of relief should present itself when the eyes remain intently fixed on one point of a binocular image in the stereoscope. But on performing the experiment carefully, it will be found, provided the pictures do not extend too far beyond the centres of distinct vision, that the image is still seen single and in relief when this condition is fulfilled. Were the theory of corresponding points true, the appearance should be that of the superposition of the two drawings, to which, however, it has not the slightest similitude. The following experiment is equally decisive against this theory.

Draw two lines inclined towards each other, as in Plate XIX. fig. 10, on a sheet of paper, and having caused them to coincide by converging the optic axes to a point nearer than the paper; look intently on the upper end of the resultant line, without allowing the eyes to wander from it for a moment. The entire line will appear single and in its proper relief, and a pin or a piece of straight wire may without the least difficulty be made to coincide exactly in position with it; or, if while the optic axes continue to be directed to the upper and nearer end, the point of a pin be made to coincide with the lower and further end or with any intermediate point of the resultant line, the coincidence will remain exactly the same when the optic axes are moved and meet there. The eyes sometimes become fatigued, which causes the line to appear double at those parts to which the optic axes are not fixed, but in such case all appearance of relief vanishes.. The same experiment may be tried with more complex figures, but the pictures should not extend too far beyond the centres of the retinæ.

Another and a beautiful proof that the appearance of relief in binocular vision is an effect independent of the motions of the eyes, may be obtained by impressing on the retinal ocular spectra of the component figures. For this purpose the drawings should be formed of broad coloured lines on a ground of the complementary colour, for instance red lines on a green ground, and be viewed either in the stereoscope or in the apparatus, fig. 6, as the ordinary figures are, taking care, however, to fix the eyes only to a single point of the compound figure; the drawings must be strongly illuminated, and after a sufficient time has elapsed to impress the spectra on the retinæ, the eyes must be carefully covered to exclude all external light. A spectrum of the object in relief will then appear before the closed eyes. It is well known that a spectrum impressed on a single eye and seen in the dark, frequently alternately appears and disappears: these alternations do not correspond in the spectra impressed on the two retinæ, and hence a curious effect arises; sometimes the right-eye spectrum will be seen alone, sometimes that of the left eye, and at those moments when the two appear together, the binocular spectrum will present itself in bold relief. As in this case the pictures cannot shift their places on the retina in whatever manner the eyes be moved about, the optic axes can during the experiment only correspond with a single point of each.

When an object, or a part of an object, thus appears in relief while the optic axes are directed to a single binocular point, it is easy to see that each point of the figure that appears single is seen at the intersection of the two lines of visible direction in which it is seen by each eye separately, whether these lines of visible direction terminate at corresponding points of the two retinæ or not.

But if we were to infer the converse of this, viz. that every point of an object in relief is seen by a single glance at the intersection of the lines of visible direction in which it is seen by each eye singly, we should be in error. On this supposition, objects before or beyond the intersection of the optic axes should never appear double, and we have abundant evidence that they do. The determination of the points which shall appear single seems to depend in no small degree on previous knowledge of the form we are regarding. No doubt, some law or rule of vision may be discovered which shall include all the circumstances under which single vision by means of non-corresponding points occurs and is limited. I have made numerous experiments for the purpose of attaining this end, and have ascertained some of the conditions on which single and double vision depend, the consideration of which, however, must at present be deferred.

Sufficient, however, has been shown to prove that the laws of binocular visible position hitherto laid down are too restricted to be true. The law of Aguilonius assumes that objects in the plane of the horopter are alone seen single; and the law of corresponding points carried to its necessary consequences, though these consequences were unforeseen by its first advocates, many of whom thought that it was consistent with the law of Aguilonius, leads to the conclusion that no object appears single unless it is seen in a circle passing through the centres of visible direction in each eye and the point of convergence of the optic axes. Both of these are inconsistent with the single vision of objects whose points lie out of the plane in one case and the circle in the other; and that objects do appear single under circumstances that cannot be explained by these laws, has, I think, been placed beyond doubt by the experiments I have brought forward. Should it be hereafter proved, that all points in the plane or in the circle above mentioned are seen single, and from the great indistinctness of lateral images it will be difficult to give this proof, the law must be qualified by the admission that points out of them do not always appear double.  
 
 

Please do not forget to visit the Stereoscopy.com Bookshop, offering the world's largest selection of books in 3D and about 3D.

Back to the Stereoscopy.com Library Index

---

Copyright © 1999 - by Stereoscopy.com and Alexander Klein. All rights reserved.