

|
Note: Footnotes of the original paper have been placed at the appropriate parts of the text, retaining their original symbols as much as possible. In order to distinguish them from the main text, they have been color-coded in brown. In the original paper, Illustrations were included on one separate engraved plate. The appropriate images are now placed at or near the respective reference in the text. The original article was published in the "Philosophical Transactions" of the Royal Society of London, Vol. 142, pp. 1 - 17. |
I. THE BAKERIAN LECTURE.—Contributions to the Physiology of Vision. – Part the Second. On some remarkable, and hitherto unobserved, Phenomena of Binocular Vision (continued). By CHARLES WHEATSTONE, F.R.S., Professor of Experimental Philosophy in King's College, London, Corresponding Member of the Academies of Science of Paris, Berlin, Brussels, Turin, Rome, Dublin, &c., of the Philosophical Society of Cambridge, the National Institute at Washington, &c.
Received and read January 15, 1852.
§ 17.
IN § 3. of the first part of my "Contributions to,the Physiology of Vision," published in the Philosophical Transactions for 1838, speaking of the stereoscope, I stated, “The pictures will indeed coincide when the sliding pannels are in a variety of different positions, and consequently when viewed under different inclinations of the optic axes ; but there is only one position in which the binocular image will be immediately seen single, of its proper magnitude, and without fatigue to the eyes, because in this position only the ordinary relations between the magnitude of the pictures on the retina, the inclination of the optic axes, and the adaptation of the eye to distinct vision at different distances, are preserved. The alteration in the apparent magnitude of the binocular images, when these usual relations are disturbed, will be discussed in another paper of this series, with a variety of remarkable phenomena depending thereon."
In 1833, five years before the publication of the memoir just mentioned, these yet unpublished investigations were announced in the third edition of HERBERT MAYO's “Outlines of Human Physiology" in the following words: — " Mr. WHEATSTONE has shown, in a paper he is about to publish, that if by artificial means the usual relations which subsist between the degree of inclination of the optic axes and the visual angle which the object subtends on the retina be disturbed, some extraordinary illusions may be produced. Thus, the magnitude of the image remaining constant on the retina, its apparent size may be made to vary with every alteration of the angular inclination of the optic axes.”
I shall resume the consideration of the phenomena of binocular vision with this subject, because the facts I have ascertained regarding it are necessary to be understood before entering on the new experiments relating to stereoscopic appearances which I intend to bring forward on the present occasion.
Under the ordinary conditions of vision, when an object is placed at a certain distance before the eyes, several concurring circumstances remain constant, and they always vary in the same order when the distance of the object is changed. Thus, as we approach the object, or as it is brought nearer to us, the magnitude of the picture on the retina increases ; the inclination of the optic axes, required to cause the pictures to fall on corresponding places of the retinæ , becomes greater; the divergence of the rays of light proceeding from each point of the object, and which determines the adaptation of the eyes to distinct vision of that point, increases ; and the dissimilarity of the two pictures projected on the retinæ also becomes greater. It is important to ascertain in what manner our perception of the magnitude and distance of objects depends on these various circumstances, and to inquire which are the most, and which the least influential in the judgements we form. To advance this inquiry beyond the point to which it has hitherto been brought, it is not sufficient to content ourselves with drawing conclusions from observations on the circumstances under which vision naturally occurs, as preceding writers on this subject mostly have done, but it is necessary to have more extended recourse to the methods so successfully employed in experimental philosophy, and to endeavour, wherever it be possible, not only to analyse the elements of vision, but also to recombine them in unusual manners, so that they may be associated under circumstances that never naturally occur.
The instrument I shall proceed to describe enables these abnormal combinations to be made in a very simple and effectual manner. Its principal object is to cause the binocular pictures to coincide, with any inclination of the optic axes, while their magnitudes on the retinæ remain the same ; or inversely, while the optic axes remain at the same angle, to cause the size of the pictures on the retinæ to vary in any manner.
Two plane mirrors inclined 90° to each other are placed together and fixed vertically upon a horizontal board. Two wooden arms move round a common centre situated on this board in the vertical plane which bisects the angle of the mirrors, and about 1 ½ inch beyond their line of junction. Upon each of these arms is placed an upright pannel , at right angles thereto, for the purpose of receiving its appropriate picture, and each pannel is made to slide to and from the opposite mirror. The eyes being placed before the mirrors, the right eye to the right mirror and the left eye to the left mirror, and the pannels being adjusted to the same distances, however the arms be moved round their centre, the distance of the reflected image of each picture from the eye will remain exactly the same, and consequently its retinal magnitude will be unchanged. But as the two reflected images do not occupy the same place when the pictures are in different positions, to cause the former to coincide the optic axes must converge differently. When the arms are in the same straight line, the images coincide while the optic axes are parallel ; and as they form a less angle with each other, the optic axes converge more to occasion the coincidence. When the arms remain in the same positions, while the pannels slide towards or from the mirrors, the convergence of the optic axes remains the same, but the magnitude of the pictures on the retinæ increases as the distance decreases. By the arrangement described, and which is represented by figs. 1 and 2 Plate I., the reflected pictures are always perpendicular to the optic axes, and the corresponding points of the pictures, when they are exactly similar, fall upon corresponding points of the retinæ . The instrument has an adjustment for otherwise inclining them if it be required.
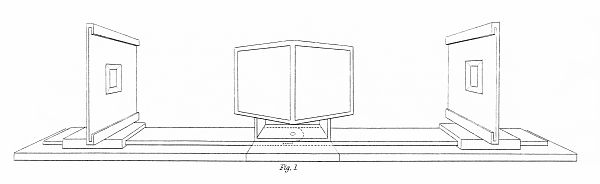
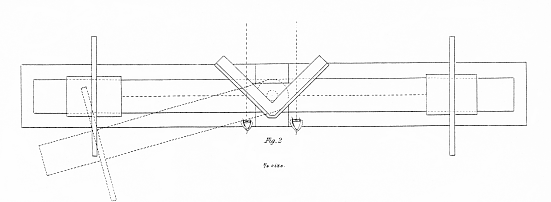
Let us now attend to the effects produced. The pictures being fixed at the same distance from the mirrors, there is a certain adjustment of the arms at which the binocular image will appear of its natural size, that is, the size we judge the picture itself to be when we look at it directly ; in this case the magnitude of the pictures on the retinæ and the inclination of the optic axes preserve their usual relation to each other. lf now the arms be moved back, so as to cause a less convergence of the axes, the image will appear to increase in magnitude until the arms are in a straight line and the optic axes are parallel ; and, on the other hand, if the arms be moved forwards, so as to form a less angle, the optic axes will converge more, and the image will appear gradually smaller. In this manner, while the retinal magnitude remains the same, the perceived magnitude of the binocular object varies through a very considerable range.
The instrument being again adjusted so that the image shall be seen of its natural size ; on sliding the pictures nearer the mirrors its perceived magnitude will be augmented, and on sliding them from the mirrors it will appear diminished in size. During these variations of magnitude the inclination of the optic axes remains the same.
The perceived magnitude of an object, therefore, diminishes as the inclination of the axes becomes greater, while the distance remains the same ; and it increases, when the inclination of the axes remains the same, while the distance diminishes. When both these conditions vary inversely, as they do in ordinary vision when the distance of an object changes, the perceived magnitude remains the same*. [* Several cases of the alteration of the perceived magnitude of objects are mentioned by Dr. R. SMITH (Complete System of Opticks , 1738, vol. ii. p. 388, and rem . 526 and 532 ) ; and Dr. R. DARWIN (Philosophical Transactions, vol. 1xxvi. p. 313) observed that when an ocular spectrum was impressed on both eyes it appeared magnified when they were directed to a wall at a considerable distance. The facts noticed by these authors are satisfactorily explained by the above considerations.]
Before I proceed further it will be proper to explain the meaning of some of the terms I employ. I call the magnitude of the object itself, the real or objective magnitude; the magnitude of the picture on the retina, the retinal magnitude ; and the magnitude we estimate the object to be from its retinal magnitude and the inclination of the optic axes conjointly, I name the perceived magnitude. I do not use the term apparent magnitude, because, according to its ordinary acceptation, it sometimes means what I call retinal, and at other times what I name perceived magnitude.
We have seen in what manner our perception of magnitude is modified by the new associations which this instrument enables us to form ; let as now examine how our perception of distance is affected by them. lf we continue to observe the binocular picture whilst it apparently increases or decreases, in consequence of the inclination of the optic axes varying while the magnitude of the impressions on the retinæ remains the same, it does not appear either to approach or to recede ; and yet if we attentively regard it in any fixed position, it is perceived to be at a different distance. On the other hand, if we continue to regard the binocular picture, enlarging and diminishing in consequence of the change of retinal magnitude while the convergence of the axes remains the same, we perceive it to approach or recede in the, most evident manner ; but on fixing the attention to it, when it is stationary, at any instant, it appears to be at the same distance at one time as it is at another.
Convergence of the optic axes therefore suggests fixed distance to the mind ; variation of retinal magnitude suggests change of distance. We may, as I have above shown, perceive an object approach or recede without appearing to change its distance, and an object to be at a different distance, without appearing to approach or recede ; these paradoxical effects render it difficult, until the phenomena are well apprehended, to know, or to express, what we actually do perceive.
It is the prevalent opinion that the sensation which accompanies the inclination of the optic axes immediately suggests distance, and that the perceived magnitude of an object is a judgement arising from our consciousness of its distance and of the magnitude of its picture on the retina. From the experiments I have brought forward, it rather appears to me that what the sensation which is connected with the convergence of the axes immediately suggests is a correction of the retinal magnitude to make it agree with the real magnitude of the object, and that distance, instead of being a simple perception, is a judgement arising from a comparison of the retinal and perceived magnitudes. However this may be, unless other signs accompany this sensation the notion of distance we thence derive is uncertain and obscure, whereas the perception of the change of magnitude it occasions is obvious and unmistakeable.
To see, in their full extent, the variations of magnitude exhibited by the instrument I have described, it is necessary to attend to the following observations.
As the inclination of the optic axes corresponding to a different distance is habitually, under ordinary circumstances, accompanied with the particular adaptation of the eyes required for distinct vision at that distance, it is difficult to disassociate these two conditions so as to see with equal distinctness the binocular picture when the optic axes are parallel, and when they converge greatly, although the pictures remain, in both cases, at the same distance from the eyes. The adaptation is, therefore, not entirely dependent on the divergence of the rays of light which proceed from the object regarded, but also, in some degree, on the inclination of the optic axes. I have acquired by practice considerable power of adjustment, or rather disadjustment , of the eyes, and can, without having recourse to artificial means, see the binocular picture distinctly when its perceived magnitude is widely different. Those to whom such an effort is painful may employ short-sighted spectacles to see the binocular picture when the eyes converge within the limit of distinct Vision for the distance at which the pictures are placed ; and long-sighted spectacles when the eyes converge beyond that limit, or become parallel.
There is a means of avoiding to a very considerable extent the influence of the adjustment of the eyes, and thereby enabling the pictures to be seen distinctly within the entire range of the inclination of the optic axes. This is by looking at the reflected images in the mirrors through two very minute apertures, not larger than fine pin-holes, placed near each eye, and illuminating the pictures by a very strong light ; sunshine in the middle of the day answers the purpose very well. By this expedient the divergence of the rays of light is greatly diminished, and the adaptation of the eyes does not materially influence the result.
§ 18.
Leaving this subject, I will now revert to the stereoscope and its effects.
Since 1838 numerous modifications of the stereoscope have occurred to me, and several ingenious arrangements have also been proposed by Sir DAVID BREWSTER and Prof. DOVE ; but there is no form of the instrument which has so many advantages for investigating the phenomena of binocular vision as the original reflecting stereoscope. Pictures of any size may be placed in it, and it admits of every kind of adjustment.
I have constructed a very portable reflecting stereoscope which is represented at fig. 3. The sides fold over the mirrors, and the mirrors then fold into a box, which is not larger than 6 inches in any of its dimensions. To avoid the second feeble reflection from the anterior surface of the silvered glass, which has a bad effect when the attention is attracted to it, I have sometimes employed reflecting prisms. The reflecting surfaces of the prisms should be silvered in order to obviate the unequal brightness of the field of view on each side of the limit of total reflection ; and as it would be too costly to employ very large prisms, they should have an adjustment to accommodate their distance to the width between the eyes of the observer.
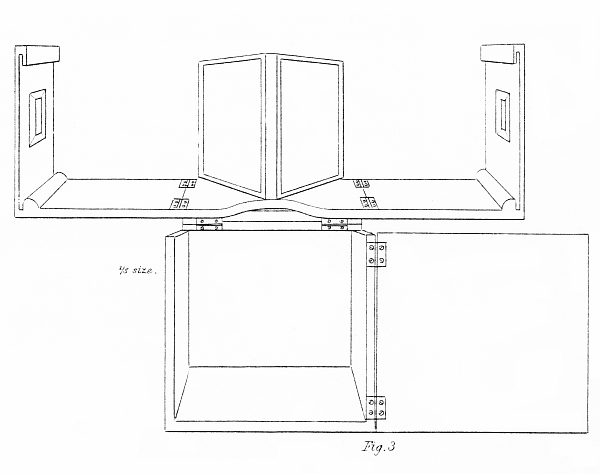
I have, for many years past, employed also another means to occasion, without any straining of the eyes, the coincidence of the pictures so that the image in relief shall appear of the same magnitude and at the same distance as the object which they represent would do if it were itself directly regarded. In this apparatus, prisms being employed to deflect the rays of light proceeding from the pictures, so as to make them appear to occupy the same place, I have called it the refracting stereoscope.
It is represented by fig. 4. It consists of a base 6 inches long and 4 inches broad, upon which stands an upright partition, 5 inches high, dividing it equally ; this partition is capable of extension by means of a slide to double the length, and carries at its upper extremity a board placed parallel to the base, and of the same dimensions. In this upper board there are two apertures an inch square, one on each side of the partition, the centres of which are 2 ½ inches from each other ; in these apertures are fixed a pair of glass prisms having their faces inclined 15°, and their refractive angles turned towards each other. The stereoscope pictures are to be placed on the base, and their centres ought not to exceed the distance of 2 ½ inches.
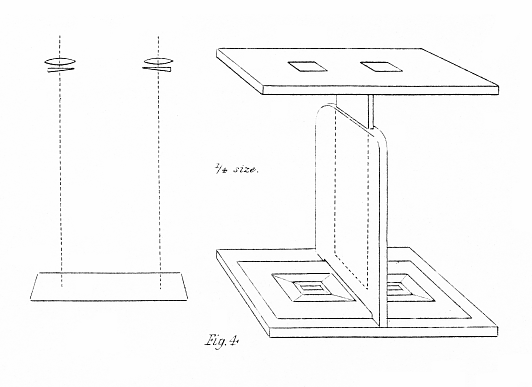
A pair of plate-glass prisms, their faces making with each other an angle of 12°, will bring two pictures, the corresponding points of which are 2 ½ inches apart, to coincidence at a distance of 12 inches, and a pair with an angle of 15° will occasion coincidence at 8 inches.
The refracting stereoscope has the advantage of portability, but it is limited to pictures of small dimensions. It is well suited for Daguerreotypes, which are usually of small size, and, on account of the nature of their reflecting surface, must be viewed in a particular direction with respect to the light which falls upon them ; whereas in the reflecting stereoscope it is somewhat difficult to render the two Daguerreotypes equally visible. For drawings and Talbotypes it however offers no advantages, though it is equally well suited for them when their dimensions are small.
Stereoscopic drawings afford a means of illustrating works with figures of three dimensions, instead of with mere plane representations. Works on crystallography, solid geometry, spherical trigonometry, architecture, machinery, &c., might be thus rendered more instructive, from the perfect counterpart of the solid figure seen from a single point of view being represented, instead of merely one of its plane projections. For this purpose the corresponding binocular figures must be engraved in parallel vertical columns, and their coalescence may be effected by viewing them through a pair of prisms, similar to those employed in the refracting stereoscope, placed in a frame at the proper distance from each other. lf the engravings should be less than 2 ½ inches apart, the prisms may be dispensed with by persons who have command over the adaptation of their eyes, particularly if they be short-sighted.
§ 19.
At the date of the publication of my experiments on binocular vision, the brilliant photographic discoveries of TALBOT, NIEPCE and DAGUERRE, had not been announced to the world. To illustrate the phenomena of the stereoscope I could therefore, at that time, only employ drawings made by the hands of an artist. Mere outline figures, or even shaded perspective drawings of simple objects, do not present much difficulty ; but it is evidently impossible for the most accurate and accomplished artist to delineate, by the sole aid of his eye, the two projections necessary to form the stereoscopic relief of objects as they exist in nature with their delicate differences of outline, light and shade. What the hand of the artist was unable to accomplish, the chemical action of light, directed by the camera, has enabled us to effect.
It was at the beginning of 1839, about six months after the appearance of my memoir in the Philosophical Transactions, that the photographic art became known, and soon after, at my request, Mr. TALBOT, the inventor, and Mr. COLLEN (one of the first cultivators of the art) obligingly prepared for me stereoscopic Talbotypes of full-sized statues, buildings, and even portraits of living persons. M. QUETELET, to whom I communicated this application and sent specimens, made mention of it in the Bulletins of the Brussels Academy of October 1841. To M. FIZEAU and M. CLAUDET I was indebted for the first Daguerreotypes executed for the stereoscope. The beautiful stereoscopic representations of statuary, architecture, machinery, natural history specimens, portraits of living persons, single and in groups, &c., which have recently been produced by M. SOLEIL and M. CLAUDET, are now too well known to the public to need more than a slight reference to them.
With respect to the means of preparing the binocular photographs (and in this general term I include both Talbotypes and Daguerreotypes), little requires to be said beyond a few directions as to the proper positions in which it is necessary to place the camera in order to obtain the two required projections.
We will suppose that the binocular pictures are required to be seen in the stereoscope at a distance of 8 inches before the eyes, in which case the convergence of the optic axes is about 18°. To obtain the proper projections for this distance, the camera must be placed, with its lens accurately directed towards the object, successively in two points of the circumference of a circle of which the object is the centre, and the points at which the camera is so placed must have the angular distance of 18° from each other, exactly that of the optic axes in the stereoscope. The distance of the camera from the object may be taken arbitrarily, for, so long as the same angle is employed, whatever that distance may be, the pictures will exhibit in the stereoscope the same relief, and be seen at the same distance of 8 inches, only the magnitude of the picture will appear different. Miniature stereoscopic representations of buildings and full-sized statues are therefore obtained merely by taking the two projections of the object from a considerable distance, but at the same angle as if the object were only 8 inches distant, that is, at an angle of 18°.
To produce the best effect, it is necessary that the pictures be so placed in the stereoscope that each eye shall see its respective picture at the proper point of sight: if this condition be not attended to, the binocular perspective will be incorrect.
For obtaining binocular photographic portraits, it has been found advantageous to employ, simultaneously, two cameras fixed at the proper angular positions.
I subjoin a Table of the inclinations of the optic axes which correspond to different distances ; it also shows the angular positions of the camera required to obtain binocular pictures which shall appear at a given distance in the stereoscope in their true relief.
Inclination of the optic axes |
2° |
4° |
6° |
8° |
10° |
12° |
14° |
16° |
18° |
20° |
22° |
24° |
26° |
28° |
30° |
Distance in inches |
71.5 |
35.7 |
23.8 |
17.8 |
13.2 |
11.8 |
10.1 |
8.8 |
7.8 |
7.0 |
6.4 |
5.8 |
5.4 |
5.0 |
4.6 |
The distance is equal to a /2 cotang θ /2; a denoting the distance between the two eyes, and θ the inclination of the optic axes.
§20.
As the inclination of the optic axes diminishes by the removal of an object to which they are directed to a greater distance, not only does the magnitude of the pictures projected by it on the retinæ proportionately diminish, but the dissimilarity of the pictures becomes less. The difference of distance between any two points of each of the pictures will diminish until the projections become sensibly similar. Under the usual circumstances attending the vision of a solid object placed at a given distance, a particular inclination of the axes is invariably accompanied by a specific pair of dissimilar projections ; and if the distance be changed, a different inclination of the axes is accompanied by another pair of projections ; but, by means of the stereoscope, we have it within our power to associate these circumstances abnormally, and to cause any degree of inclination of the axes to coexist with any dissimilarity of the two pictures. To ascertain experimentally what takes place under these circumstances M. CLAUDET prepared for me a number of Daguerreotypes of the same bust, taken at a variety of different angles, so that I was enabled to place in the stereoscope two pictures taken at any angular distance from 2° to 18°, the former corresponding with a distance of about 6 feet, and the latter with a distance of about 8 inches. The effect of a pair of near projections seen with a distant convergence of the optic axes, is to give an undue elongation to lines joining two unequally distant points, so that all the features of a bust appear to be exaggerated in depth. The effect, on the contrary, of a pair of distant projections, seen with a near convergence of the axes, is to give an undue shortening to the same lines, so that the appearance of a bas-relief is obtained from the two projections of the bust. The apparent dimensions in breadth and height remain in both cases the same.
§21.
To reproduce the conditions of the binocular vision of a solid object as completely as possible by means of its two plane projections, it is necessary, as I have before stated, that the projections shall be such as correspond exactly with the inclination of the optic axes under which they are viewed. I have already shown in § 20 what takes place when this condition is not strictly observed, and I may add that the mind is not unpleasantly affected by a considerable incongruity in this respect; on the contrary, the effect in many cases seems heightened by viewing the solid appearance, intended for a determinate degree of inclination of the axes, under an angle several degrees less ; the reality is as it were exaggerated. When the optic axes are parallel, in strictness there should be no difference between the pictures presented to each eye, and in this case there would be no binocular relief ; but I find that an excellent effect is produced when the axes are nearly parallel by pictures taken at an inclination of 7° or 8°, and even a difference of 16° or 17° has no decidedly bad effect.
This circumstance enables us to combine the ideal amplification arising from viewing pictures placed near the eyes under a small inclination, or even parallelism, of the optic axes mentioned in § 17, with the perception of solidity arising from the dissimilarity of the projections ; for this purpose, the pictures in the refracting stereoscope, or their reflected images in the reflecting instrument, must be viewed through lenses the focal distance of which is equal to the distance between them and the pictures ; the perceived magnitude of the binocular image will increase with the nearness of the pictures, and depends almost entirely on the disassociation of the retinal magnitude from its usually accompanying inclination of the optic axes, the actual magnifying power of the lenses having a very small influence.
The sole use of the lenses is to render the rays of light parallel, which it is necessary they should be for distinct vision when the optic axes are parallel. When the reflecting stereoscope is employed, this means of magnifying the effect is not of much utility, as pictures of any size may be adapted to that instrument. But in the case of the refracting stereoscope it may be advantageously made use of. By combining lenses with the refracting stereoscope, described in § 18, Daguerreotypes somewhat wider than the width between the eyes may be employed. Sir DAVID BREWSTER has used, to effect the same purpose, semi-lenses with their edges directed towards each other, which serve at the same time to render the rays less convergent and slightly to displace the pictures towards each other. Two corresponding Daguerreotypes, each not exceeding in breadth the width between the eyes, being placed close to each other, and viewed with lenses of short focal distance, will even without the aid of the prisms give an apparently highly magnified binocular image in bold relief.
There is a peculiarity in such images worthy of remark ; although the optic axes are parallel, or nearly so, the image does not appear to be referred to the distance we should, from this circumstance, suppose it to be, but it is perceived to be much nearer, and indeed more so, as the pictures are nearer the eyes, though the inclination of the optic axes remains the same, and should therefore suggest the same distance ; it seems as if the dissimilarity of the projections, corresponding as they do to a nearer distance than that which would be suggested by the former circumstance alone, alters in some degree the perception of distance.
I recommend, as a convenient arrangement of a refracting stereoscope for viewing Daguerreotypes of small dimensions, the instrument represented, fig. 4, shortened in its length from 8 inches to 5, and lenses of 5 inches focal distance placed before and close to the prisms.
§ 22.
I now proceed to another subject — to the consideration of those phenomena which I have termed Conversions of Relief.
In § 5 of my first memoir I noticed the remarkable circumstance, that when the drawing intended to be seen by the right eye is presented to the left eye in the stereoscope, and vice versâ , a totally different solid figure is perceived to that seen before the transposition. I called this the converse figure, and showed that it differs from the normal figure in the circumstance, that those points which appear the most distant in the latter, appear the nearest in the former.
The pictures being, in the first place, presented directly to their corresponding eyes, as in the refracting stereoscope, and exhibiting therefore the resultant image in its normal relief, the conversion of the relief may be effected in three different ways, — 1st, by transposing the pictures from one eye to the other, as mentioned above ; 2ndly, by reflecting the pictures, while they remain presented to the same eye, as in the reflecting stereoscope ; and 3rdly, by inverting the position of the pictures without transposing them.
The following considerations will explain the cause of the conversion of relief in the preceding cases.
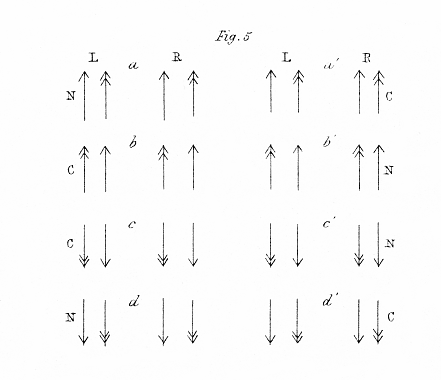
lf two different objects, or parts of an object (fig. 5 a ), have a greater lateral distance between them on the right-hand picture than that which they have on the left-hand picture, the optic axes must converge more to make the left-hand than to make the right-hand objects coincide, and the left-hand object will appear the nearest.
lf the pictures be now transposed from one eye to the other (fig. 5 a' ), the greatest distance will be between the corresponding points of the picture presented to the left eye ; the optic axes must therefore converge less to make the left-hand objects coincide, and the right-hand object will appear the nearest.
lf the pictures, remaining untransposed , be each separately reflected (fig. 5 b ), the relative distances of the corresponding objects remain the same to each eye, and the left-hand object will still appear nearest ; but in consequence of the lateral inversion of the objects in each picture by reflexion , that which was previously on the left will now be on the right, and therefore, the object which before appeared nearest, will now appear farthest.
When the pictures are turned upside down, still remaining untransposed (fig 5 c ), the objects are reversed with respect to the right and left, in the same manner as they are when reflected, and the lateral distances between the objects remaining the same to each eye, precisely the same conversion of relief is produced as in the preceding case, except that the resultant image is inverted. The diagram (fig. 5) represents all the possible changes of the two binocular pictures ; those marked N show the normal relief, and those marked C the converse relief.
But it may be asked why, if the reflection or inversion of the binocular pictures of an object gives rise to the mental idea of the converse relief, the same converse relief is not observed when the object itself is reflected in a mirror, or inverted. The reason is this ; that in the former cases the projections to each eye are separately reflected or inverted, still remaining presented to the same eye, whereas, by the reflection or inversion of the object itself, not only are the projections reflected or inverted, but they are also transposed from one eye to the other ; and these circumstances occurring simultaneously reproduce the normal relief.
Fig. 6 will render this evident in the case of reflexion : A is the object, B its reflexion in the mirror CD ; RB and LB are the directions in which the right and left eyes view the reflected image respectively, and l A and r A the directions in which the eyes would view the corresponding face of the object directly.
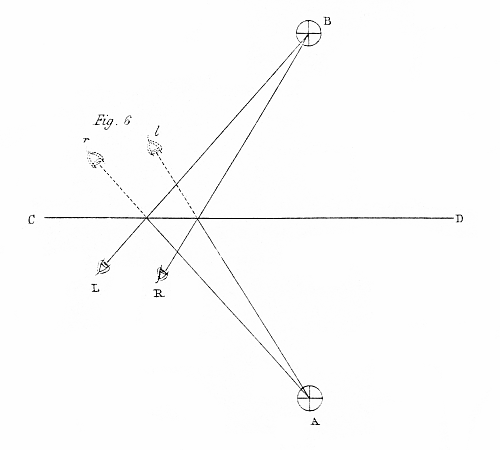
In the case of an inverted object, it is obvious that that projection which was before seen by the right eye must be seen by the left eye, and the contrary.
It is possible to make this normal or converse relief appear while one of the pictures remains constantly presented to the same eye. This result may be thus obtained. Having taken a photograph of the object, which should be one the converse of which has a meaning, take two others at the same angular distance (say 18°), one on the right side, the other on the left side of the original. Of the three pictures thus taken, if the middle one be presented to the right eye, and the left picture to the left eye, a normal relief will be seen ; but if the right picture be presented to the left eye, the other remaining unchanged, a converse relief will be seen. In like manner, if the middle picture be presented to the left eye, and the right picture to the right eye, a normal relief will appear ; but if the left picture be presented to the right eye, the converse relief will present itself. It must be observed, that the normal and converse reliefs , when the same picture remains presented to the same eye, belong to two different positions of the object.
§ 23.
Hitherto I have taken into consideration only those cases of the conversion of relief which are exhibited by binocular pictures in the stereoscope, when they are transposed, reflected or inverted ; I shall now proceed to show how phenomena of the same kind may be elicited by regarding objects themselves, by means of an instrument adapted for the purpose. As this instrument conveys to the mind false perceptions of all external objects, I have called it the Pseudoscope. It is represented by fig. 7, and is thus constructed : two rectangular prisms of flint glass, the faces of which are 1.2 inch square, are placed in a frame with their hypothenuses parallel, and 2.1 inches from each other ; each prism has a motion on an axis corresponding with the angle nearest the eyes, so that they may be adjusted that their bases may have any inclination towards each other ; and the frame itself is adjustable by a hinge at a , in order to bring the prisms nearer each other to suit the eyes of the observer.
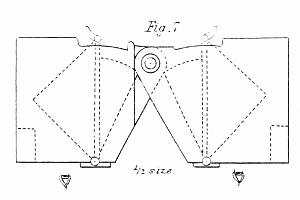
The instrument being held to the eyes, and adjusted to an object, so that it shall appear single, each eye will see a reflected image of that projection of the object which would be seen by the same eye without the pseudoscope. This is exactly the contrary of what occurs when the eyes regard the reflected image of an object in a looking- glass ; the left eye then sees the reflected image of the right-hand projection, and the right eye the reflected image of the left projection, as shown by fig. 6.
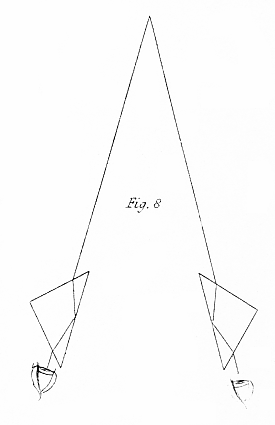
Plane mirrors cannot be substituted for the reflecting prisms, for this reason ; the refraction of the rays of light at the incident and emergent surfaces of the prisms enables the reflexion of an object to be seen when the object is even behind the prolongation of the reflecting surface, as shown at fig. 8, and thus the reflected binocular image may be seen in the same place as the object itself, whereas the images cannot be made by means of plane mirrors thus to coincide.
When the pseudoscope is so adjusted as to see a near object while the optic axes are parallel, to view a more distant object with the same adjustment, the axes must converge, and the more so as the object is more distant ; all nearer objects than that seen when the axes are parallel, will appear double, because the optic axes can never be simultaneously directed to them. lf this instrument be so adjusted that very distant objects are seen single when the eyes are parallel, all nearer objects will appear double, because the optic axes can never converge to make their binocular images coincide. lf the attention is required to be directed to an object at a particular distance, the best mode of viewing it with the pseudoscope is to adjust the instrument so that the object shall appear at the proper distance and of its natural size. In this case the more distant objects will appear nearer and smaller, and the nearer objects will appear more distant and larger.
In ordinary vision, whenever the distance of an object varies, the magnitude of the picture on the retina, and the degree of convergence of the optic axes, always maintain a constant relation to each other, both increasing or decreasing together ; and the perceived magnitude, suggesting to the mind the real magnitude of the object, in consequence thereof remains the same. The instrument I described in § 17 shows what illusions arise when the usual relations of these elements of our perceptions are disturbed, by causing one to remain constant while the other varies. The pseudoscope exhibits the still more curious illusions, which result from combining these elements inversely, so that as an object becomes nearer, its larger picture on the retina is accompanied by a less convergence of the optic axes. With the pseudoscope we have a glance, as it were, into another visible world, in which external objects and our internal perceptions have no longer their habitual relation with each other.
I will now proceed to describe some of the illusions produced by the aid of this instrument. Those which may be strictly designated conversions of relief, in which the illusive appearance has the same relation to that of the real object as a cast to a mould, or a mould to a cast, are very readily perceived. I must however remark, that it is necessary to illuminate the object equally, so as to allow no lights or shades to appear upon them, for their presence has a considerable influence on the judgement, and is one of the principal causes of the perception of the proper relief when a single eye is employed.
The inside of a tea-cup appears as a solid convex body ; the effect is more striking if there are painted figures within the cup.
A china vase, ornamented with coloured flowers in relief, presents a very remarkable appearance ; we apparently see a vertical section of the interior of the vase, with painted hollow impressions of the flowers.
A small terrestrial globe appears as a concave hemisphere ; on turning it round on its axis, it was curious to see different portions of the spherical map appear and disappear in a manner that nothing in external nature can imitate.
A bust regarded in front becomes a deep hollow mask ; the appearance when regarded in profile is equally striking.
A framed picture hanging against a wall, appears as if imbedded in a cavity made in the wall.
A medal, or the impression of a seal, is perfectly converted into a representation of the die from which it has been struck ; and, on the other hand, the mould or die of a medal, or an engraved seal, becomes a fac -simile of the medal or raised impression. It will also be observed, that if the medal be placed on a flat surface, as a sheet of paper, it will appear sunk beneath the surface ; and if it be placed in a hollow of the same size, it will appear to stand above the surface as much as it actually is below it.
These appearances are not always immediately perceived ; and some much more readily present themselves than others. Those converse forms which have a meaning, and resemble real forms we have been accustomed to see, are those which are the most easily apprehended. Viewed with the pseudoscope, notwithstanding the inversion of the pictures on the retina, the natural appearance of the object continues to intrude itself, when sometimes suddenly, and at other times gradually, the converse occupies its place. The reason of this is, that the relief and distance of objects is not suggested to the mind solely by the binocular pictures and the convergence of the optic axes, but also by other signs, which are perceived by means of each eye singly ; among which the most effective are the distributions of light and shade and the perspective forms which we have been accustomed to see accompany these appearances. One idea being therefore suggested to the mind by one set of signs, and another totally incompatible idea by another set, according as the mental attention is directed to the one and abstracted from the other, the normal form or its converse is perceived. This mental attention is involuntary ; no immediate effort of the will can call up one idea while the other continues to present itself, though the transition may be facilitated by intentionally removing some of the signs which suggest the preponderating idea ; thus the converse form being perceived, closing either eye will most frequently cause an instant reversion to the normal form ; and always, if the monocular signs of relief are sufficiently suggestive.
I know of nothing more wonderful, among the phenomena of perception, than the spontaneous successive occurrence of these two very different ideas in the mind, while all external circumstances remain precisely the same. Thus a small statuary group, an elegant and beautiful object, without any apparent cause becomes converted into another totally dissimilar object uncouth in appearance, and which gives rise to no agreeable emotions in the mind ; yet in both cases all the sensations that intervene between objective reality and ideal conception continue unchanged.
The effects of the pseudoscope I have already mentioned, may be strictly called conversions of relief, because the illusive appearance is in each case the converse impression of the relief of the real object. If, however, the object consists of parts detached from and behind each other, the preceding term is inappropriate to denote the effects which result, but the more general expression conversion or inversion of distance may be employed to designate them. I proceed to call attention to a few such effects.
Skeleton figures of geometrical solids, as cubes, pyramids, &c., readily show their converse.
Two objects at different distances, being simultaneously regarded, the most remote will appear the nearest and the nearest the most remote.
An ivory foot rule, held immediately before the eyes a little inclined to the horizon with its remote end elevated, appears inclined in the opposite way, its nearer end elevated, and as if the observer were looking at its lower surface. Its form also undergoes a change. Since the nearest end, the retinal magnitude of which is the largest, appears farthest from the eyes, and the nearest end, the retinal magnitude of which is greatest, appears near the eyes, the rule will no longer be perceived to be rectangular, but trapezoidal. If the rule be placed horizontally, and it be regarded with the pseudoscope at an angle of 45°, it will appear with the form just described standing vertically.
Any object placed before the wall of a room will appear behind the wall, and as if an aperture of the proper dimensions had been made in the wall to allow it to be seen ; if the object be illuminated by a candle, its shadow will appear as far before the object as in reality it is behind.
The appearance of a plant is very remarkable ; as the branches which are farthest from the eye are perceived to be the nearest, those parts which are actually obscured by the branches before them, appear broken away and allow the parts apparently behind them to be seen. A flowering shrub before a hedge appears to be transferred behind it ; and a tree standing outside a window may be brought visibly within the room in which the observer is standing.
I have before observed that the transition from the normal to the converse perception is often gradual ; I will give one instance of this as an illustration. The object was a page of medallions embossed on card-board, and the raised impressions were protected from injury by a thick piece of mill-board having apertures in it made to correspond to each medallion. The page was placed horizontally, illuminated by a candle placed beyond it, and looked at through the pseudoscope at an angle of 45° ; for the first moment the page appeared as it would have done without the instrument ; soon after the medallions appeared level with the upper surface, and the shadows on the upper parts of the circular apertures were converted into deep depressions as if cut out with a tool ; they next, from horizontal, became vertical, each standing erect on the horizontal plane, and immediately afterwards the reliefs were all changed into hollows ; finally, the page itself stood vertical, but with that change of form which I indicated in the case of the rule, the upper edge appearing much shorter than the lower edge: the series of changes being now complete, the final form remained constant as long as the object was regarded.
In endeavouring to analyse the phenomena of converse perception, it must be borne in mind that the transposition of distances has reference only to distances from the retinæ , not to absolute horizontal distances in space. Thus, if a straight ruler be held in the vertical plane perpendicular to the optic base, and also inclined 45° to the horizon so that its upper end shall be the most distant, when the eyes are directed horizontally towards it, the rule will appear exactly in the converse position. lf the rule be now removed lower down in the same vertical plane, its inclination remaining unchanged, so that to look upon it the plane of the optic axes must be inclined 45°, it will appear unaltered in position, because its two pictures are parallel on the retinæ , and the optic axes would require the same convergence to make the upper and lower ends coalesce. The rule being removed still lower down, instead of its position being apparently reversed, it will appear to have a greater inclination on the same side than the object itself has. In the first case the more distant end is actually farthest from the eyes ; in the second the near and remote ends are equally distant ; and in the third the nearest end is most distant.
Attention to what I have just stated will explain many anomalous circumstances which occur when the eyes are differently directed towards the same object. It may also be necessary to remark, that the conversion of distance takes place only within those limits in which the optic axes sensibly converge, or the pictures projected on the retinæ are sensibly dissimilar. Beyond this range there is no mutual transposition of the apparent distances of objects with the pseudoscope ; a distant view therefore appears unchanged.
Some very paradoxical results are obtained when objects in motion are viewed through the pseudoscope. When an object approaches, the magnitude of its picture on the retinæ increases as in ordinary vision, but the inclination of the optic axes, instead of increasing, becomes less, as I have already explained. Now an enlargement of the picture on the retina invariably suggests approach, and a less convergence of the optic axes indicates that the object is at a greater distance ; and we have thus two contradictory suggestions. Hence, if two objects be placed side by side at a certain distance before the eyes, and one of them be moved forwards, so as to vary its distance from the other, its continually enlarging picture on the retina makes it appear to come towards the eyes, as it actually does, while at the same time it appears at every step at a greater distance beyond the fixed object ; from one suggestion the object appears to approach, from the other to have receded. I again observe that retinal magnitude does not itself suggest distance, but from its changes we infer changes of distance.
I have hitherto only described the pseudoscope constructed with two reflecting prisms. This is the most convenient apparatus for effecting the conversion of distance and relief that has occurred to me ; but other means may be employed, which I will briefly mention.
1st. Two plane mirrors are placed together so as to form a very obtuse angle towards the eyes of the observer ; immediately before them the object is to be placed at such distance that a reflected image shall appear in each mirror. The eyes being placed before and a little above the object, must be caused to converge to a point between the object and the mirrors ; the right-hand image of the left eye will then unite with the left-hand image of the right eye, and the converse relief will be perceived. The disadvantages of this method are that only particular objects can be examined, and it requires a painful adaptation of the eye to distinct vision.
2ndly. Place between the object and each eye a lens of small focal distance, and adjust the distances of the object and the lenses so that distinct inverted images of the object shall be seen by each eye ; on directing the eyes to the place of the object the two images will unite, and the converse relief be perceived. As the rays of light proceeding from the images have a greater divergence than those which would proceed from the point to which the optic axes are directed, long-sighted persons will see the binocular image more distinctly by wearing a pair of short-sighted spectacles. In this experiment the field of view is very small on account of the distance at which it is necessary to place the lenses from the eyes ; but I have been enabled in this manner to see beautifully the converse relief of a small ivory bust and of other small objects, which however should be inverted in order to see them direct.
3rdly. The inverted images of the lenses, instead of being received immediately by the eyes as just described, may be thrown on a plate of ground glass as in the case of the ordinary camera-obscura, and may be then caused to unite by the means employed in any form of the refracting stereoscope.
§ 24.
The cases of the conversion of relief when the object is regarded with one eye only, some of which were known more than a century ago, were taken into consideration and endeavoured to be explained by me in § 11 of the first part of this memoir, and Sir DAVID BREWSTER* [* Transactions of the Royal Society of Edinburgh, vol. xv. p. 365 and 657.] has published some interesting and instructive observations on the same subject ; I will therefore not revert to this matter here, but only to say that I have myself never observed the conversion of relief when looking with both eyes immediately on a solid object, and if it has been observed by others under such circumstances, I should be inclined to attribute the effect to an inequality in the impressions on the two eyes so that one only is attended to. But the plane shaded representation of a solid object, the relief of which is not very deep, may easily be made to appear at will either as the solid which it is intended to represent or as its converse, even when both eyes are employed. This effect is strikingly observed in the glyptographic engravings of medals of low relief, and depends entirely on whether the light is so placed that it would cast the same shadows on the real object as are represented in the picture, or that it would cast shadows in the opposite direction. In the former case the picture appears with the relief it was intended to suggest ; in the latter with the converse relief. I have observed similar effects with Daguerreotypes of medallions and cameos, and with carefully shaded drawings of simple objects.
 |
|

| Back to the Stereoscopy.com Library Index |
